Ein technischer Blick auf das Mapping virtueller Welten für reale Räume

Im Februar 2017 hat MediaMonks gemeinsam mit dem World Wildlife Fund, dem ArtScience Museum und dem Google Zoo die groß angelegte Mixed-Reality-Erfahrung "Into The Wild" gestartet
Damit sollten die Menschen in Singapur die verheerenden Auswirkungen der Abholzung erfahren und mehr über einige der am stärksten bedrohten Arten der Welt und ihre Lebensräume lernen.
Es war das weltweit erste Tango-fähige Smartphone Lenovo Phab 2 Pro und führte die Besucher durch personalisierte digitale Abenteuer, die mit Augmented Reality (AR) im Erdgeschoss des Ausstellungsraums begannen, bevor sie in die vollständige virtuelle Realität (VR) übergingen.
Am Ende des Erlebnisses kehren die Besucher zur AR zurück und gehen in den vierten Stock, wo sie unter anderem einen virtuellen Baum pflanzen.
Das Singapore ArtScience Museum wurde auf über 1.000 Quadratmetern in einen virtuellen, interaktiven Regenwald verwandelt. Damit ist es das größte AR-Erlebnis der Welt und das zweite AR-Museumserlebnis, das mit Google Tango entwickelt wurde.
Und das war nicht einfach. Aus technischer Sicht standen wir vor der großen Herausforderung, einen virtuellen Regenwald akkurat und reibungslos auf einen physischen und dynamischen Museumsraum abzubilden. Wir mussten sicherstellen, dass die Wände mit den Bäumen und die Korridore mit den Pfaden des Waldes übereinstimmten und dass wir die bestehenden Ausstellungen und Inszenierungen des Museums umgehen konnten.
Damit können wir die Ausrichtung abschließen. Und da Tango die Koordinaten des Geräts in ecef-Koordinaten zurückmeldet, können wir die entsprechenden Unity-Koordinaten leicht berechnen. Effektiv aktualisieren wir die Unity-Kamera mit jedem Tango-Update, das wir mit dieser Transformation erhalten.
Darüber hinaus wurde für jeden gepflanzten virtuellen Baum ein echter Baum in Rimbang Baling gepflanzt, einem der letzten unberührten Regenwälder in Sumatra, in dem der vom Aussterben bedrohte Sumatra-Tiger lebt. im ersten Monat des Projekts wurden 5000 neue Bäume zugesagt.
Ich hoffe, dass wir damit die Vorstellungskraft aktueller und angehender Entwickler anregen können, noch aufregendere AR/VR-Erlebnisse zu schaffen, die sich an der realen Welt orientieren. Geht hinaus und erobert!
Wie haben wir es also geschafft?
Wenn Sie die reale Welt mit virtuellen Objekten erweitern, ist es zunächst einmal wichtig, dass das Gerät, das Ihre Ansicht wiedergibt (z. B. ein Smartphone, ein Monitor, eine CAVE oder ein am Kopf befestigtes Gerät), genau weiß, wo es sich in der realen Welt befindet.
Dazu muss das Gerät seine Position und Ausrichtung in einem dreidimensionalen Raum kennen.
Im Fall von Tango, wo die Augmentierung auf einem Kamerafeed basiert, müssen die Position und die Orientierung des Rendering-Geräts in der realen Welt liegen. Nur wenn die Position und Ausrichtung eines Tango-Geräts genau und schnell genug gemeldet wird, ist eine korrekte Augmented Reality möglich.
Die Tatsache, dass Google Tango dies für Sie erledigt, ist sehr cool, weil es Entwicklern ermöglicht, reale Orte in ihrer eigenen virtuellen Welt zu erweitern, was sich von Snapchat-ähnlicher AR unterscheidet, bei der Sie zum Beispiel Hasenohren an Ihren Kopf anbauen.
Mit Augmentierungen, die an die reale Welt gebunden sind, kann man potenziell gemeinsame AR-Erlebnisse schaffen, die sich um Wahrzeichen drehen und diese einbeziehen.
In diesem Fall konnten wir das ArtScience Museum in einen üppigen virtuellen Regenwald verwandeln, und aus der Perspektive des Nutzers wird die Erkundung des Regenwalds so natürlich wie die Erkundung des Museums selbst, da jeder Korridor oder jedes Hindernis in der virtuellen Welt einem Korridor oder Hindernis in der realen Welt entspricht.

In die Wildnis

In die Wildnis

In die Wildnis
In die Wildnis

In die Wildnis

In die Wildnis
Google Tango-Koordinaten
Wir haben Unity3D verwendet, um unsere virtuelle Welt zu erstellen. Zu Beginn haben wir unseren Unity-Entwicklern versichert, dass sie sich keine Gedanken über die Ausrichtung machen müssen und die virtuelle Welt in jeder beliebigen Position oder Ausrichtung gestalten können, solange sie maßstabsgetreu ist.
Entwickler, die mit geografischen Informationssystemen (GIS) vertraut sind, wissen, dass es viele Koordinatensysteme gibt, die als "Datumsangaben" bezeichnet werden. In der Vergangenheit haben viele Institute ihre eigenen Systeme entwickelt, aber seit der Einführung von GPS haben die USA das WGS84 entwickelt, das am häufigsten für kommerzielle Geräte verwendet wird.
Das Besondere an diesem Koordinatensystem ist, dass es kartesisch ist, in Metern rechnet und den Erdmittelpunkt als Ausgangspunkt verwendet. Dies ist wichtig, da Google Tango in einer korrekt kartierten Umgebung seine genaue Position und Ausrichtung auf dem Globus angeben kann und diese in WGS84 angibt.
Google Tango nennt diese Koordinaten ecef-Koordinaten, also werden wir sie auch ecef nennen.
Bestimmung der korrekten Annäherung
Der nächste Schritt besteht darin, sicherzustellen, dass sich unsere Unity-Welt mit der realen Welt überschneidet, damit wir Augmented Reality erreichen können. Hierfür gibt es zwei Lösungsansätze.
- Transformieren (Verschieben+Drehen) der Unity-Welt, damit sie auf den ecef-Koordinaten des Museums sitzt.
- Transformieren (Verschieben+Drehen) der Koordinaten des ecef Tango-Geräts in die Koordinaten der Unity-Welt.
Die Ansätze sind zu 80 Prozent gleich, denn in beiden Fällen müssen Sie die Transformation von der virtuellen (Unity) in die reale (ecef) Welt berechnen. Der Unterschied liegt jedoch darin, ob man die virtuelle Welt auf die reale Welt überträgt (Ansatz eins) oder ob man die reale Kamera auf die virtuelle Welt überträgt (Ansatz zwei).
Um herauszufinden, welcher Ansatz der beste ist, mussten wir sehen, wie diese Koordinaten in einem realen Anwendungsfall aussehen. Hier sind einige Beispiele dafür, wie Unity-Koordinaten aussehen:
Objekt A: [10.000, 63.250, -11.990]
Objekt B: [-92,231, 33,253, -62,123]
Im Gegensatz dazu sind unten zwei Beispiele für das Aussehen von ecef-Koordinaten zu sehen:
Hilversum MediaMonks HQ 2. Stock in der Nähe des Fahrstuhls: [3899095,5399920414; 353426,87901774078; 5018270.6428830456]
Singapur ArtScienceMuseum vor dem Kassenshop: [-1527424,0031555446; 6190898,8392925877; 142221,77658961274]
Offensichtlich handelt es sich bei den ecef-Koordinaten um recht große Zahlen. In der Tat ist es klar, dass Gleitkommazahlen mit einfacher Genauigkeit (oder Fließkommazahlen) eine Menge Probleme damit haben werden.
Ohne zu sehr ins Detail zu gehen, ist es wichtig zu wissen, dass die Durchführung von Arithmetik mit Zahlen um 10-6 mit Zahlen um 106 einen erheblichen Genauigkeitsverlust bedeutet.
Außerdem führt kein Weg an der Tatsache vorbei, dass ein Großteil der 3D-Programmierung im Bereich von 10-3 bis 103 stattfindet (man denke an Transformations-, Modell-, Ansichts- oder Projektionsmatrizen).
Um dies besser zu verstehen, empfehle ich, sich dieses Video anzusehen, da es diesen Punkt perfekt veranschaulicht. Es zeigt einen Kampfjet, der in der Nähe des Ursprungs [0; 0; 0] startet und von einer Kamera verfolgt wird. Während die eigene Position immer größer wird (ebenso wie die Position der Kamera), werden die Gleitkommaberechnungen immer ungenauer.
Stellen Sie sich vor, wie groß der Fehler wäre, wenn die Koordinaten Ihrer Kamera wie die oben gezeigten ecef-Koordinaten wären Sie würden fein skalierte Rotationswerte mit sehr großen Positionswerten kombinieren. Der Fehler im Ergebnis wird enorm sein.

AR macht nicht ganz so viel Spaß, wenn die Augmentierung nicht sorgfältig durchgeführt wird.
Hinzu kommt die Tatsache, dass Unity so programmiert ist, dass es mit Fließkommazahlen arbeitet (und nicht mit Double-Precision Floating Points oder Doubles), und wir können uns keine großen Fehler in AR leisten. Es ist daher klar, dass Ansatz eins nicht durchführbar ist. Das liegt daran, dass die Kamera relativ nahe am Ursprung bleiben muss, um Präzisionsfehler zu vermeiden.
Wir fahren also mit Ansatz zwei fort, der darin besteht, die Koordinaten des ecef Tango-Geräts in Unity-Weltkoordinaten zu transformieren.
Finden Sie die Transformation
Bei Transformationen zwischen Koordinatensystemen in der 3D-Grafik werden in der Regel Translations- (Positions-), Orientierungs- und Skalierungswerte ermittelt.
Jedes dieser drei Konzepte wirkt im 3D-Raum, daher müssen sie die Positionierung, Drehung und Skalierung für jede der drei Achsen (x, y und z) beschreiben. Somit haben wir neun Werte zu ermitteln.
Die neun Unbekannten sind ein Hinweis darauf, wie viele Gleichungen Sie benötigen, um diese neun Unbekannten zu finden. Dies ist wichtig, um zu bestimmen, wie viele Koordinaten der realen Welt benötigt werden, um unsere virtuelle Welt zu verankern.
Unsere ursprüngliche Idee war es, eine Transformation zu erstellen, die alle drei Konzepte (Translation, Rotation und Skalierung) abdeckt. Aufgrund von Schwierigkeiten und der Tatsache, dass wir in der Lage waren, unsere virtuelle Welt maßstabsgetreu zu gestalten, beschlossen wir jedoch, die Berücksichtigung des Maßstabs aufzugeben und uns nur auf Translation und Rotation zu konzentrieren.
Das bedeutet, dass wir jetzt nur noch sechs Unbekannte finden müssen.
Berechnen der Transformationsmatrix
An diesem Punkt der Lösung dieser Aufgabe müssen wir eine Transformationsmatrix finden, die nur die Lage und Drehung berücksichtigt. Glücklicherweise wurde dieses Problem bereits millionenfach von Informatikstudenten gelöst.
Wenn Sie einfach in Google suchen, finden Sie unzählige Beispiele dafür, wie man einen starren Körper von einem Koordinatensystem in ein anderes transportiert. Dieses Beispiel führt Sie zu 90 Prozent ans Ziel.
Bei der Suche nach einer Transformationsmatrix geht es um die Minimierung der Summe der Fehlerquadrate zwischen zwei Datenpunktsätzen. Die folgende Methode ist auf dieses Problem zugeschnitten, da sie Rotation und Translation getrennt behandelt.
Konzeptionell gehen wir so vor, dass wir einen Punkt in der realen Welt auswählen und sagen, dass dieser Punkt einem anderen Punkt in der virtuellen Welt entspricht.
Im Grunde sind die Welten an diesem Punkt miteinander verankert. Wie Sie sich jedoch vorstellen können, können sich die Welten bei der Wahl eines einzigen Punktes als Anker immer noch um den Anker drehen, so dass sie die meiste Zeit über falsch ausgerichtet sind.
Um die virtuelle Welt perfekt auf die reale Welt zu setzen, braucht man also mindestens mehrere Anker. Je nach der Anzahl der Unbekannten, die man zu finden versucht, benötigt man eine gleiche oder größere Anzahl von Gleichungen.
Gleichungen können aus bekannten Paaren (in diesem Fall ecef und Unity-Koordinaten) abgeleitet werden. In diesem Fall sind insgesamt 3 Paare (oder Anker) ausreichend, um eine vollständige 3D-Transformationsmatrix zu finden.
Die Idee ist, dass man N Punkte (mindestens drei) in der realen Welt auswählt und deren ecef-Koordinaten findet. Dann geht man in die virtuelle Welt und platziert einen Punkt an den entsprechenden virtuellen Orten (also insgesamt N). Für das Museumsprojekt haben wir 10 leicht zu findende Orientierungspunkte an der Basis jeder Säule im Museum verwendet.
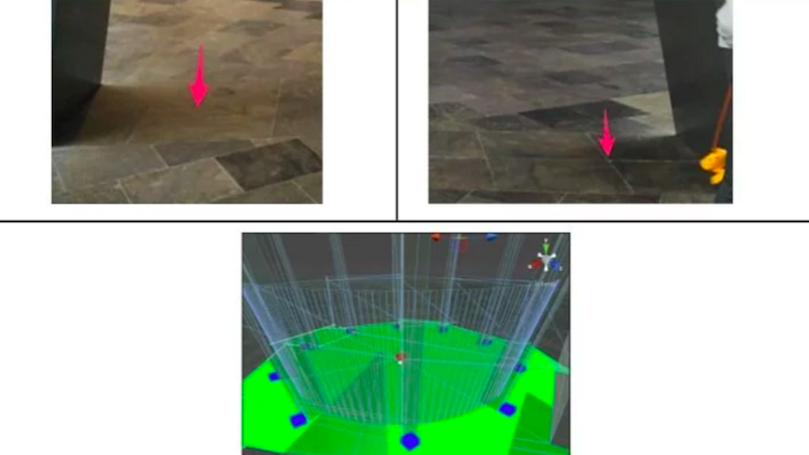
Oben: zwei ecef-Koordinaten, die wir in der realen Welt gemessen haben, und unten: ihre Pendants in der virtuellen Welt.
Hierfür haben wir eine Bibliothek eines Drittanbieters namens Math.Net verwendet, die es uns ermöglicht, lineare Algebra mit Doubles durchzuführen. Sie müssen diesen Code nur einmal zu Beginn des Programms ausführen.
Das Ergebnis ist, dass wir nun 10 Ecef-Koordinaten und 10 Unity-Koordinaten in Form eines Kreises haben, was 10 Koordinatenpaare ergibt. Der nächste Schritt besteht nun darin, die in diesem Artikel besprochenen Schritte anzuwenden und eine Transformationsmatrix zu finden, mit der wir einen Punkt vom Ecef-Raum in den Unity-Raum transformieren können.
Bei der Umsetzung dieses Vorhabens sind wir auf einige Probleme gestoßen. Zum Beispiel ist Unity ein linkshändiges Koordinatensystem, während ecef rechtshändig ist. Und der Artikel, auf den wir oben verwiesen haben, verwendet auch eine Zeilen-Hauptreihenfolge, während die Bibliothek eine Spalten-Hauptreihenfolge verwendet.
Das macht das Füllen, Transponieren und die Multiplikation von Matrizen unterschiedlich. All diese Probleme konnten wir durch sorgfältige Überlegungen und den Versuch, nicht zu viele Schritte gleichzeitig zu unternehmen, überwinden.
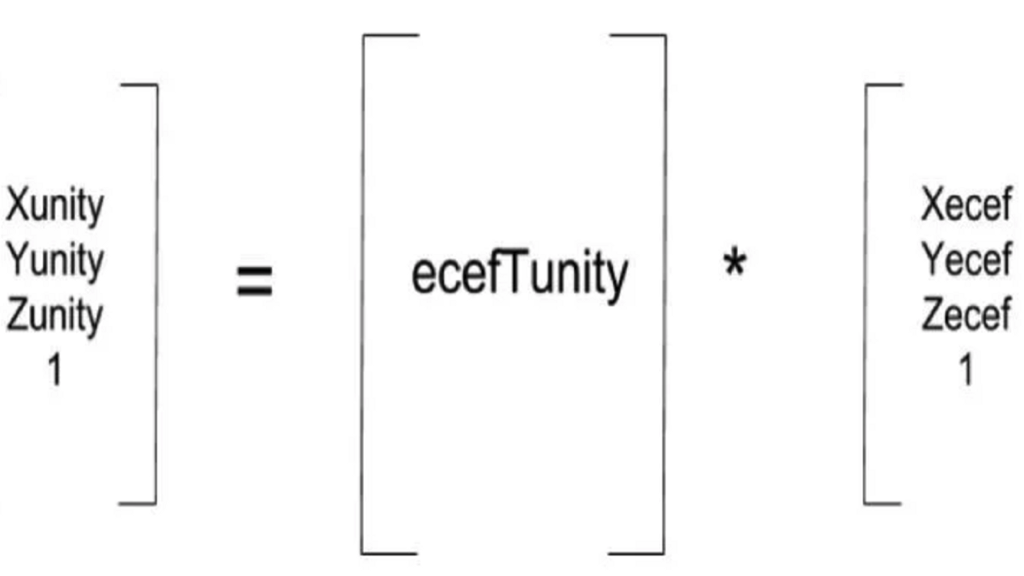
Anwenden der Transformation
Nach dem vorherigen Schritt haben wir eine Transformationsmatrix, die wir ecefTunity nennen können (oder unityTecef, je nachdem, wie Sie die Matrix berechnet haben). Die Transformation eines Punktes im ecef-Raum in den unity-Raum ist also so trivial wie:
Verwandte
Themen
-
![A portrait of a woman in profile, facing right, with her blonde hair blurred as if in motion. She wears a black turtleneck against a dark, moody background featuring abstract magenta and purple rectangles and vertical lines. Her face is illuminated, while the rest of the image has a blurred, dreamlike quality.]()
Blog-Beitrag
Was 2025 über KI enthüllt wurde und was 2026 möglich sein wird Von Monks 5 min Lesezeit -
![A pale pink "New message" window with thin black outlines floats against a pastel gradient background of lavender, pink, and peach. Inside the window are "To" and "Subject" fields, and a rounded rectangular "Send" button in the bottom right corner. The window has a simple close "X" icon in the top right.]()
Blog-Beitrag
Aufbau von Vertrauen in den E-Mail-Posteingang und einer starken Absenderreputation durch disziplinierte Warming-Strategien Von Bridget Creach 9 min Lesezeit -
![search]()
Blog-Beitrag
Die Antwort Engine Battles: Navigieren durch die ChatGPT-Anzeigeneinführung Von Tory Lariar 4 min Lesezeit
Schärfen Sie Ihre Kanten in einer Welt, die nicht warten will
Melden Sie sich an, um E-Mail-Updates mit umsetzbaren Erkenntnissen, aktuellen Forschungsergebnissen und bewährten Strategien zu erhalten.
Monks benötigt die Kontaktinformationen, die Sie uns zur Verfügung stellen, um Sie über unsere Produkte und Dienstleistungen zu informieren. Sie können sich jederzeit von diesen Mitteilungen abmelden. Informationen darüber, wie Sie sich abmelden können, sowie über unsere Datenschutzpraktiken und unsere Verpflichtung zum Schutz Ihrer Daten finden Sie in unserer Datenschutzrichtlinie.